反応速度と半減期が「スッと解けるようになる」コツ

――3倍則と炭素14で、指数（べき）を味方につける

反応速度や半減期の問題は、知識量よりも**「同じ増え方・減り方が何回起きたか」**を数えられるかどうかで安定します。
ここを押さえると、頭の中で無理に処理しなくても、手順どおりに答えにたどり着けます。

ポイントは3つです。

• 「3倍」が何回起きたかを、温度差から確定する
• 「半分」が何回起きたかを、割合から確定する
• “定数”と“濃度”の役割を分けて、混ぜない

---

1. まず見抜く：これは「指数の問題」です

反応速度・半減期でよくある条件は、見た目は違っても中身は同じです。

• 一定の割合で増える（例：10℃上がるごとに3倍）
• 一定の割合で減る（例：半減期＝半分になる）

どちらも本質は、**「同じ倍率が何回くり返されたか」**を数えることです。
この“回数”が決まれば、あとは指数（べき）でまとめられます。

---

2. 反応速度の3倍則：「回数」を温度差から確定する

例：10℃上がるごとに反応速度が3倍

20℃→60℃に上げると、反応速度は何倍ですか？

ここで大事なのは、いきなり 3⁴ を書くことではなく、「4回」を温度差から作ることです。

• 温度上昇：60−20＝40℃
• 10℃ごとに3倍 → 回数＝40÷10＝4回
• したがって 3倍が4回 → 3⁴＝81倍

「指数」は、くり返しの省略記号

3⁴ は新しいルールではなく、単に

• 3×3×3×3

を短く書いたものです。
「×3が何回か」を先に確定できれば、指数は“圧縮表記”として自然に出てきます。

---

3. 頭の中でやらない：温度軸と矢印で“回数”を可視化する

3倍則は、暗算で一気に処理しようとすると崩れやすい分野です。
そこで、次のように段階を図示して回数を見える化すると安定します。

• 20→30→40→50→60 と区切る
• 「10℃ごとに3倍」を、矢印ごとに1回として数える
• 4本の矢印が見えれば、3⁴に迷いません

この「図示・段階計算」は、反応速度だけでなく、半減期にもそのまま効きます。

---

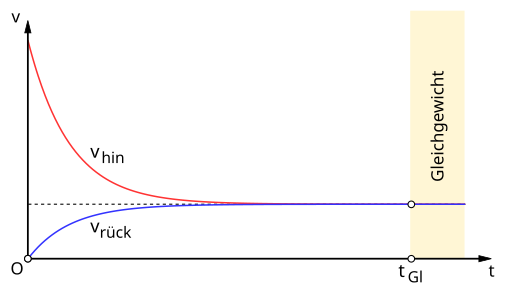
4. 反応速度“定数”k：濃度と混ぜない（ここがよく落とし穴）

反応速度の文章問題では、次のような誤解が頻出です。

「濃度が大きいほど反応速度定数kも大きい」

これは基本的に誤りです。
一定温度なら、kは温度で決まり、濃度とは別物として整理します。

• 反応速度 v は濃度に影響されやすい（例：v＝k[A]… の [A] 側）
• しかし kそのものは、主に温度依存の値として扱う

「定数」という名前どおり、濃度と同じ棚に置かないのがコツです。

---

5. 半減期：割合を (1/2)ⁿ に直せば終わる

半減期の問題は、やることが実はかなり固定です。

1. 与えられた割合を (1/2)ⁿ に直す
2. n（半分が何回起きたか）を数える
3. 半減期×n で時間（年数）にする

“よく出る割合”は、回数に変換して覚えると速い

• 1/2 ＝ (1/2)¹ → 1回
• 1/4 ＝ (1/2)² → 2回
• 1/8 ＝ (1/2)³ → 3回
• 1/16＝ (1/2)⁴ → 4回

この対応が見えていると、式を作る前に勝負が決まります。

---

6. 炭素14（¹⁴C）で確認：8分の1＝「半分が3回」

年代測定の典型例として、次がよく出ます。

遺跡の木片の¹⁴C存在比が、生きている植物の 8分の1 だった。何年前？

8分の1は

• 1/8 ＝ (1/2)³

なので、「半分」が3回起きたと読み取れます。
炭素14の半減期は 5730年なので、

• 5730×3＝17190年前

となります。

---

7. ¹⁴Cが「なぜ14なのか」も一度だけ整理しておく

炭素は原子番号6なので、陽子数は6です。
質量数14は「陽子＋中性子」なので、

• 中性子数＝14−6＝8

と求まります。

この整理は、放射性同位体の話題で「核の中で何が増えたのか」を見失わないための最小限の下準備になります。

---

8. それでも迷ったら：logを使う前に“回数”で粘る

半減期は、割合が 1/8 や 1/16 のように (1/2)ⁿ に直せる形なら、回数で勝てます。
log（対数）の操作は、割合が中途半端で「半分の回数」が整数にならないときにだけ必要になります（入試でも、まずは回数で処理できる形が多いです）。

---

典型的に崩れるポイント（先に潰すチェックリスト）

• 温度差を見ずに、回数を感覚で決める
• k（定数）と濃度を同じ棚に置いてしまう
• 半減期で、割合を (1/2)ⁿ に直さず式に突っ込む

---

まとめ：2つの“翻訳”ができれば安定します

• 倍率の翻訳：a倍がn回 → aⁿ
• 半分の翻訳：割合 → (1/2)ⁿ に直して回数を数える

反応速度と半減期は、暗記の量ではなく、回数を読み取る技術で伸びる分野です。
「指数（べき）は、くり返しを短く書く道具」と捉えた瞬間から、問題が整って見えてきます。