【体系解説】濃度変換の計算

読んだ後に学びがあったと感じた方は、♡をタップしていただけると嬉しいです。

※この記事は、電子書籍『一問一答 理論化学1｜原子の構造、化学結合、物質量と化学反応式』の内容の一部をもとに作成しています。

濃度計算はこの4タイプだけ── 型を覚えれば迷わない。

濃度計算が苦手な理由の多くは、「与えられた数値をどう使えばいいか」が見えないからです。
しかし実際には、4つの型を押さえれば解法の道筋がはっきりします。

このページでは、「なんとなく計算していた」状態から、「必要な情報をもとに意味のある式を組み立てられる」状態に変わるための最初の一歩を紹介します。

📘単位とモノを見極める！

まずは問題を見たら、「何が与えられていて、何を求めるのか？」を見抜くクセをつけましょう。

たとえば、

溶質の物質量（mol）と溶液の体積（L）が与えられている

→ モル濃度を求めればよい

このように、単位を見て反応するのが第一歩です。

g ⇄ mol ⇄ L の変換は、分子量・密度などを使って自由に行き来できるようになります。

・密度（g/cm³）… 1cm³あたりの質量。例：水は約1.0 g/cm³

📘「濃度計算の型」を図で押さえよう

どの問題も、基本の型を使えばスッと式が立てられます。ここではその全体像を見ておきましょう。

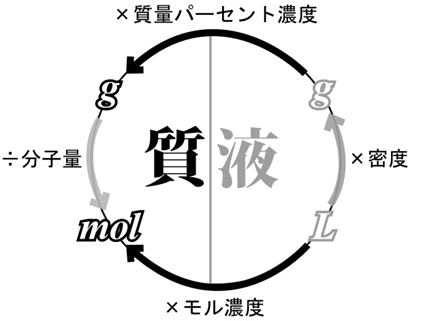
図中の矢印は、質量・物質量・体積の間での変換方法を表します。

・溶液の質量g × 質量パーセント濃度 ＝ 溶質の質量g
・溶質の質量g ÷ 分子量 ＝ 溶質の物質量mol
・溶液の体積mL（cm³）× 密度g/cm³ ＝ 溶液の質量g

📘 モル濃度と質量パーセント濃度のちがいは？

どちらも「溶質 ÷ 溶液」の形ですが、割るものの単位がちがいます。

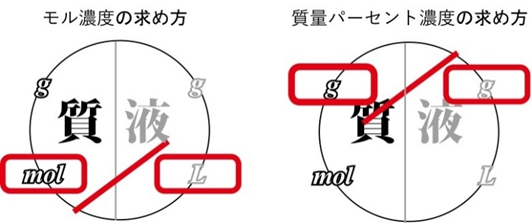
・モル濃度：mol / L（体積ベース）
・質量パーセント濃度：g / g（質量ベース）

濃度は割合です。
「全体に対してどれだけ入っているか」を、体積か質量のどちらで測るかの違いです。

📘希釈・混合では「変わらない量」がカギ！

水でうすめたり、溶液どうしを混ぜる問題では、「変わらないもの」を使って式を立てます。

よく使う『3つの変わらない量』

① 溶質の質量g
② 溶質の物質量mol
③ 混合後の溶液全体の質量g

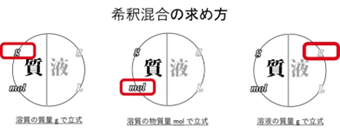
この図では「何を基準にして式を立てるか」を整理しています。薄める前後で変わらない量を見つけられると、どんな問題でもスムーズに式が立てられます。

ここで少し立ち止まって考えてみましょう。体積からmol、molからgへと、型の矢印どおりに進めただけです。慣れてしまえば、計算はとてもシンプルです。

濃度計算は型で覚える！まずは図になじもう

・単位とモノをセットで確認する
・モル濃度は mol/L、質量パーセント濃度は g/g
・希釈・混合は「変わらない量」を使う
・式は「型」の矢印に沿って組み立てる

続きは電子書籍で！濃度の問題もスラスラ解けるように

この記事で紹介したのは、第7章のごく一部です。続きでは、

・各型の使い分け練習と公式の見極め方
・入試レベルの応用（希釈×濃度×密度の複合）
・つまずきやすいポイントのQ\&A
・モル⇄質量⇄体積⇄個数の変換マップ（図付き）

などを扱います。

学びがあったと感じた方は、♡をタップしていただけると嬉しいです。